The inverses of exponential functions are logarithmic functions, and an exponential function may be represented in logarithmic form. In the same way, all logarithmic functions can be recast in exponential form. Logarithms are incredibly useful because they allow us to manipulate very huge numbers while modifying much smaller ones.
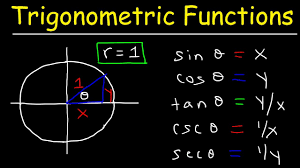
The domain input value for the fundamental six trigonometric functions is a right triangle angle, and the numeric answer is the range. The domain of the trigonometric function f(x) = sin (commonly known as the ‘trig function’) is the angle represented in degrees or radians, and the range is [-1, 1]. Similarly, all other functions have a domain and range. Trigonometric functions are extensively used in calculus, geometry, and algebra.
Let us get familiar with different functions, formulas, values and identities of Trigonometric Functions and its Log.
Trigonometric Functions Formulas
Using the sides of a right-angled triangle, we may get the values of the trig functions using certain formulas. We utilize the abbreviated form of these functions to write these formulas. Sine is abbreviated as sin, cosine is abbreviated as cos, tangent is shorthand as tan, secant is abbreviated as sec, and cotangent is abbreviated as cot. The following are the basic formulas for finding trigonometric functions:
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
- sec θ = Hypotenuse/Base
- cosec θ = Hypotenuse/Perpendicular
- cot θ = Base/Perpendicular
Trigonometric Functions Values
Trigonometric functions have a domain that is measured in degrees or radians. These standard values of trig functions at specified angles are also known as main values, and they are commonly employed in calculations. A unit circle was used to derive the principal values of trigonometric functions. All trigonometric formulas are satisfied by these values.
Trigonometric Functions Identities
Reciprocal identities, Pythagorean formulae, sum and difference of trig functions identities, formulas for multiple and submultiple angles, and sum and product of identities are all examples of trigonometric functions identities. The ratio of sides of a right-angled triangle can be used to generate all of the formulas below. The basic trigonometric function formulas can be used to derive the higher formulas. Reciprocal identities are frequently utilized to make trigonometric problems easier to understand.
Properties of Logarithmic Functions
When working with complex log functions, logarithmic function qualities come in handy. All of the standard arithmetic operations on numbers are turned into a new set of operations within logarithms. Within the logarithmic functions, the product of two numbers equals the sum of the logarithmic values of the two functions. Similarly, division operations are translated into the difference between the two numbers’ logarithms. In the following sections, we’ll go through the most important properties of log functions.
- loga/b = log a – log b
- loga 1 = 0
- loga a = 1
Graphing Logarithmic Functions
Have an idea whether you’ll get an increasing or decreasing curve as the answer before constructing a log function graph. The curve is growing if the base is greater than one, and lowers if the base is less than one. The steps for graphing logarithmic functions are as follows:
- Determine the domain and the range.
- By setting the parameter to 0, you can find the vertical asymptote. It’s worth noting that a log function has no horizontal asymptote.
- Use the attribute log a 1 = 0 to substitute some x value that makes the argument equal to 1. We now have the x-intercept.
- Use the property log a a = 1 to replace a value of x that makes the argument equal to the base. We’d get a point on the graph as a result of this.
- Extend the curve on both sides with regard to the vertical asymptote by joining the two points (from the previous two steps).